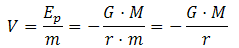Del mismo modo que se concibe el campo gravitatorio para
interpretar las fuerzas gravitatorias a partir de la perturbación que cada masa
produce en el espacio, interesa introducir el concepto de potencial
gravitatorio, para caracterizar, en relación con la energía potencial
gravitatoria de un sistema, cada punto del espacio.
El procedimiento seguido para obtener el valor de esta
magnitud en cualquier punto alrededor de un cuerpo de masa M, comienza también
colocando ahí una pequeña masa de prueba o masa testigo, m. Seguidamente divide
la energía potencial del sistema (formado por ambas masas, M y m) entre la masa
testigo, m. Por tanto, el potencial gravitatorio (V) creado por un
cuerpo esférico (de masa M), a una cierta distancia (r), es:
Igual que la energía, el potencial gravitatorio es una
magnitud escalar. Igual que el campo, su valor sólo depende de la masa del
cuerpo que lo produce y de la distancia del punto considerado a dicho cuerpo.
La expresión del potencial gravitatorio indica que, como la
energía, el potencial es mayor cuanto más lejos se esté de la masa que lo
produce. En consecuencia, el potencial decrece en la misma dirección en la que
se incrementa el campo.
Este concepto se observa en el dibujo adjunto, donde se
representan las líneas del campo gravitatorio que produce un cuerpo y tres
superficies equipotenciales (en cada una de ellas el potencial gravitatorio
vale lo mismo en todos sus puntos), 1, 2 y 3, de tal forma que V1 > V2 >
V3. Las líneas del campo gravitatorio proceden del infinito y se dirigen hacia
el cuerpo, atravesando a las superficies equipotenciales, en dirección
perpendicular a ellas, y en el sentido en que el potencial decrece.