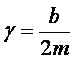Se denominará m a
la masa e y a la distancia entre la
posición de la masa y la posición de equilibrio. Se supondrá que la fuerza del
resorte es estrictamente proporcional al desequilibrio: F=-ky (ley de Hooke). F es la fuerza y k la
constante elástica del resorte. El signo negativo indica que cuando y es positiva la fuerza está dirigida
hacia las y negativas.
Aplicando la 2ª ley de Newton: SF=ma
Y resolviendo la ecuación
diferencial anterior obtenemos la ecuación del movimiento armónico simple:
Oscilador armónico amortiguado:
Añadiendo pérdidas de
energía, se consigue modelar una situación más próxima a la realidad. Así,
nótese que la oscilación descrita en el apartado anterior se prolongaría
indefinidamente en el tiempo (la sinusoide que describe la posición no converge
a cero en ningún momento). Una situación más verosímil se corresponde con la
presencia de una fuerza adicional que frena el movimiento. Esa fuerza puede ser
constante (pero siempre con signo tal que frene el movimiento). Es el caso de
rozamientos secos: la fuerza no depende ni de la velocidad ni de la posición.
Otra situación que se produce en la realidad es que la fuerza sea proporcional
a la velocidad elevada a una potencia, entera o no. Así sucede cuando la fuerza
que frena proviene de la viscosidad o de las pérdidas aerodinámicas. Se tratará
únicamente el caso más simple, es decir, cuando la fuerza sea proporcional a la
velocidad. En este caso la fuerza será:
Fuerza viscosa proporcional
a la velocidad: F = - bv
Donde b es
un coeficiente que mide el amortiguamiento debido a la viscosidad. Si es pequeño, el sistema está poco amortiguado.
Nótese el signo negativo que indica, como antes, que si la velocidad es positiva,
la fuerza tiene la dirección opuesta a la velocidad.
Aplicando la 2ª ley de
Newton: SF=ma, con este término complementario la ecuación
diferencial del sistema es:
Resolviendo la ecuación
diferencial:
Tiene tres tipos de soluciones
según el valor de (b2 - 4km):
- Si b2 - 4km < 0 el
sistema oscila con amplitud decreciente (amortiguamiento débil o subcrítico)
- Si b2 - 4km = 0 el sistema
tiene amortiguamiento crítico.
- Si b2 - 4km > 0 el
sistema está sobreamortiguado (amortiguamiento
fuerte o supercrítico)
Oscilador con amortiguamiento débil (b2 -
4km < 0)
Oscilaciones amortiguadas. En este caso,
que es más interesante, tenemos un oscilador que oscila alrededor de la posición
de equilibrio con amplitud decreciente.
La solución es:
como antes, A y j0 son constantes que dependen de las condiciones
iniciales.
La pulsación es:
donde
La pulsación del sistema
amortiguado wf es un poco menor que la pulsación del sistema no
amortiguado w porque la fuerza que lo amortigua, frena la masa y
la retarda. Y la amplitud de la sinusoide está controlada por la exponencial Ae- gt
