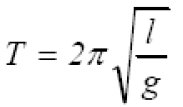Un péndulo simple se define como una partícula de masa m
suspendida del punto O por un hilo inextensible de longitud L y de masa
despreciable.
Un péndulo simple se define como una partícula de masa m
suspendida del punto O por un hilo inextensible de longitud L y de masa
despreciable.
Si la partícula se desplaza a una posición θ (ángulo que
hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar. El péndulo
describe una trayectoria circular, un arco de una circunferencia de radio L.
Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.
Las fuerzas que actúan sobre la partícula de masa m son dos: el peso mg y la tensión T del hilo.
Descomponemos el peso en la acción simultánea de sus dos
componentes, mg·sen θ en la dirección
tangencial y mg·cos θ en la dirección radial.
Ecuación del movimiento en la dirección radial:
La aceleración de la partícula es an = v2/L dirigida
radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se escribe: man = T - mg cos θ
Conocido el valor de la velocidad v en la posición angular q podemos determinar la tensión T del
hilo.
La tensión T del hilo es máxima, cuando el péndulo pasa por
la posición de equilibrio, Tmáx = mg + mv2/L
La tensión T del hilo es mínima, en los extremos de su trayectoria cuando la
velocidad es cero, Tmín = mg cos θ
Ecuación del movimiento en la dirección tangencial:
La aceleración de la partícula es at = dv/dt
La segunda ley de Newton se escribe: m at = -mg·sen θ
La relación entre la aceleración tangencial at y la
aceleración angular α es at = α·L La ecuación del movimiento se escribe en
forma de ecuación diferencial:
Cuando el ángulo θ es
pequeño entonces, sen θ = θ , comparando la ecuación con la del movimiento armónico simple, el péndulo describe oscilaciones armónicas cuya
ecuación es:
de frecuencia angular ω2 = g/L, o de periodo: