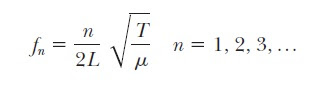Analicemos el fenómeno de interferencia que se produce
cuando dos ondas armónicas que viajan en direcciones opuestas con una misma frecuencia f y con una misma amplitud A se encuentran. (Es el caso de una onda que se encuentra con su onda reflejada)
y para la onda que viaja hacia la izquierda tenemos:
Y(x,t)= A sen (ωt + kx) (sentido izquierdo)
Aplicando el principio de superposición y relaciones trigonométricas obtenemos:
Y(x,t) = Y1+Y2 = 2A cos kx cos ωt
Onda estacionaria (no viaja):
Onda que viaja a la derecha, onda que viaja hacia la izquierda y onda estacionaria que no viaja:
Siendo la amplitud de la onda estacionaria*:
A´ = 2A cos kx
Nodos
Se llaman así a los puntos en los que la amplitud es cero.
Se caracterizan por cos kx = 0, lo cual se cumple cuando kx=(2n+1)π/2, por tanto:
x = λ/4, 3λ/4, 5λ/4.....
Los nodos de vibración son equidistantes, dos nodos
consecutivos distan una semilongitud de onda.
Vientres
Son los puntos del medio donde la amplitud es máxima, es
decir, 2A
Se caracterizan por cos kx = +/- 1, lo cual se cumple cuando kx=nπ, por tanto:
x = 0, λ/2, λ, 3λ/2, 2λ.....
Los vientres son equidistantes, dos vientres consecutivos
distan una semilongitud de onda.
Consecuencia: La distancia entre un nodo y un vientre
consecutivo es un cuarto de longitud de onda.
La frecuencia (f) se obtiene dividiendo la velocidad de propagación (v) entre la longitud de onda (l):
f = v/λ
* También podemos escribir la amplitud de la onda estacionaria con la función SENO, llegando a los mismos resultados
ONDAS ESTACIONARIAS EN UNA CUERDA FIJA POR DOS EXTREMOS:
Una cuerda de longitud L fija en los
extremos. La cuerda tiene un conjunto de modos normales de vibración, cada uno
con una frecuencia característica. Los extremos de la cuerda deben de ser
nodos ya que estos puntos se encuentran fijos.
El primer modo de vibración será
aquél en el que la longitud de la cuerda sea igual a media longitud de onda L= λ/2. Para el segundo modo de vibración, la longitud de la cuerda será igual a
una longitud de onda, L= λ. Para el tercer modo, L=3λ /2, y así sucesivamente.
En consecuencia, las longitudes de onda de los diferentes modos de vibración se
puede expresar como:
λn = 2L/n (cuerda fija por dos extremos) n = 1,2,3,...
Recordando la relación (f = v/λ) entre la velocidad de propagación (v), que depende del medio, la longitud de onda (λ) y la frecuencia de la onda (f), obtenemos las frecuencias de resonancia:
fn = nv/2L
n = 1 sonido fundamental o primer armónico
n = 2, 3, 4, 5, ... armónicos
ARMÓNICOS EN LA CUERDA DE UNA GUITARRA
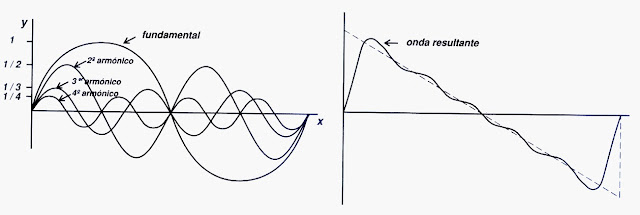
Los armónicos son una parte importante de toda nota. Cada vez que se pulsa una cuerda de la guitarra, empieza a vibrar según un patrón complicado, y el sonido que produce se compone de varios elementos.
El componente básico del sonido es la fundamental, que es el elemento que más fuerte se oye, y que identificamos con la tonalidad de la nota o tono. Es el sonido producido cuando la cuerda vibra en una sola onda en toda su longitud. Al mismo tiempo, la cuerda produce una serie de armónicos o parciales superiores, que son tonos con frecuencias múltiplos de la frecuencia de la fundamental, y que se generan por que la cuerda también vibra simultáneamente en ondas más cortas.
Se puede considerar que las ondas estacionarias no son ondas de propagación sino los distintos modos de vibración de la cuerda, el tubo con aire, la membrana, etc.
Cuando se produce una vibración sonora dentro de un tubo (abierto o cerrado) sólo hay ciertas frecuencias a las que se producen ondas estacionarias que se llaman frecuencias de resonancia. La más baja se denomina frecuencia fundamental, y las demás se denominan armónicos (múltiplos enteros de la fundamental (doble, triple, ...)). Es el caso típico de los instrumentos de viento (flauta, oboe, clarinete, trompeta, tuba, aparato fonador humano, etc.).
Cuando se produce una vibración sonora dentro de un tubo (abierto o cerrado) sólo hay ciertas frecuencias a las que se producen ondas estacionarias que se llaman frecuencias de resonancia. La más baja se denomina frecuencia fundamental, y las demás se denominan armónicos (múltiplos enteros de la fundamental (doble, triple, ...)). Es el caso típico de los instrumentos de viento (flauta, oboe, clarinete, trompeta, tuba, aparato fonador humano, etc.).
Ondas estacionarias en un tubo abierto en ambos extremos.
Si llamamos
n al número de armónico, se puede expresar la longitud de la onda armónica, λn,
en función de la longitud del tubo, L, con esta sencilla fórmula: L = nλ/2
λn = 2 L / n
(dos extremos abiertos)
Recordando la relación (f = v/λ) entre la velocidad de propagación (v), que depende del medio, la longitud de onda (λ) y la frecuencia de la onda (f), obtenemos las frecuencias de resonancia:
fn = nv/2L
n = 1 sonido fundamental o primer armónico
n = 2, 3, 4, 5, ... armónicos
La mayoría de los instrumentos de viento son de extremos
libres. La excepción la encontramos en los órganos, la flauta de pan o el
clarinete. Cuando una onda estacionaria está confinada a un espacio con los dos
extremos libres, coincide un vientre con la zona abierta.
Ondas estacionarias en un tubo
cerrado en uno de sus extremos:
Si llamamos
n al número de modo de vibración, se puede expresar la longitud de la onda
resonante, λn, en función de la longitud del tubo, L, con esta sencilla fórmula: L= (2n – 1) λ/4
λn = 4 L / (2n – 1) (un extremo cerrado)
Recordando la relación (f = v/l) entre la velocidad de propagación (v), que depende del medio, la longitud de onda (λ) y la frecuencia de la onda (f), obtenemos las frecuencias de resonancia:
fn = (2n – 1)v/4L
n = 1 sonido fundamental o primer armónico
n = 2, 3, 4, 5, ... armónicos
