Teoría sobre el origen y la formación del Universo (Big
Bang)
El hecho de que el universo esté en expansión se deriva de
las observaciones del corrimiento al rojo realizadas en la década de 1920 y que
se cuantifican por la ley de Hubble. Dichas observaciones son la predicción
experimental del modelo de Friedmann-Robertson-Walker, que es una solución de
las ecuaciones de campo de Einstein de la relatividad general, que predicen el
inicio del universo mediante un big bang.
El "corrimiento al rojo o redshift" es un fenómeno observado
por los astrónomos, que muestra una relación directa entre la distancia de un
objeto remoto (como una galaxia) y la velocidad con la que éste se aleja. Si
esta expansión ha sido continua a lo largo de la vida del universo, entonces en
el pasado estos objetos distantes que siguen alejándose tuvieron que estar una
vez juntos. Esta idea da pie a la teoría del Big Bang; el modelo dominante en
la cosmología actual.
La Ley de Hubble establece que el corrimiento al rojo de una galaxia es proporcional a la distancia a la que está.
Ho: constante de Hubble
D: distancia entre galaxias
c: velocidad de la luz
z: corrimiento al rojo, incremento en la
longitud de onda (l) de radiación electromagnética recibida por un detector
comparado con la longitud de onda emitida por la fuente.
La relación velocidad-distancia, siendo v la velocidad de recesión debida a la expansión del universo, puede formularse así:
v = Ho D
Durante la era más temprana del Big Bang, se cree que el
universo era un caliente y denso plasma. Según avanzó la expansión, la
temperatura decreció hasta el punto en que se pudieron formar los átomos. En
aquella época, la energía de fondo se desacopló de la materia y fue libre de
viajar a través del espacio. La energía remanente continuó enfriándose al
expandirse el universo y hoy forma el fondo cósmico de microondas. Esta
radiación de fondo es remarcablemente uniforme en todas direcciones,
circunstancia que los cosmólogos han intentado explicar como reflejo de un
periodo temprano de inflación cósmica después del Big Bang.
El examen de las pequeñas variaciones en el fondo de
radiación de microondas proporciona información sobre la naturaleza del
universo, incluyendo la edad y composición. La edad del universo desde el Big
Bang, de acuerdo a la información actual proporcionada por el WMAP de la NASA, se
estima en unos 13.700 millones de años, con un margen de error de un 1% (137
millones de años). Otros métodos de estimación ofrecen diferentes rangos de
edad, desde 11.000 millones a 20.000 millones.
Sopa Primigenia
Hasta hace poco, la primera centésima de segundo era más
bien un misterio, impidiendo los científicos describir exactamente cómo era el
universo. Los nuevos experimentos en el RHIC, en el Brookhaven National
Laboratory, han proporcionado a los físicos una luz en esta cortina de alta
energía, de tal manera que pueden observar directamente los tipos de
comportamiento que pueden haber tomado lugar en ese instante.
En estas energías, los quarks que componen los protones y
los neutrones no estaban juntos, y una mezcla densa supercaliente de quarks y
gluones, con algunos electrones, era todo lo que podía existir en los
microsegundos anteriores a que se enfriaran lo suficiente para formar el tipo
de partículas de materia que observamos hoy en día.
Protogalaxias
Los rápidos avances acerca de lo que pasó después de la
existencia de la materia aportan mucha información sobre la formación de las
galaxias. Se cree que las primeras galaxias eran débiles "galaxias
enanas" que emitían tanta radiación que separarían los átomos gaseosos de
sus electrones. Este gas, a su vez, se estaba calentando y expandiendo, y tenía
la posibilidad de obtener la masa necesaria para formar las grandes galaxias
que conocemos hoy.
Destino Final
El destino final del universo tiene diversos modelos que
explican lo que sucederá en función de diversos parámetros y observaciones. A
continuación se explican los modelos fundamentales más aceptados:
Big Crunch o la Gran Implosión
Es posible que el inmenso aro que rodeaba a las galaxias sea
una forma de materia que resulta invisible desde la Tierra. Esta materia oscura
tal vez constituya el 99% de todo lo que hay en el universo.
Si el universo es suficientemente denso, es posible que la
fuerza gravitatoria de toda esa materia pueda finalmente detener la expansión
inicial, de tal manera que el universo volvería a contraerse, las galaxias
empezarían a retroceder, y con el tiempo colisionarían entre sí. La temperatura
se elevaría, y el universo se precipitaría hacia un destino catastrófico en el
que quedaría reducido nuevamente a un punto.
Algunos físicos han especulado que después se formaría otro
universo, en cuyo caso se repetiría el proceso. A esta teoría se la conoce como
la teoría del universo oscilante.
Hoy en día esta hipótesis parece incorrecta, pues a la luz
de los últimos datos experimentales, el Universo se está expandiendo cada vez
más rápido.
Big Rip o Gran Desgarramiento
El Gran Desgarramiento o Teoría de la Eterna Expansión,
llamado en inglés Big Rip, es una hipótesis cosmológica sobre el destino último
del universo. Este posible destino final del universo depende de la cantidad de
energía oscura existente en el Universo. Si el universo contiene suficiente
energía oscura, podría acabar en un desgarramiento de toda la materia.
El valor clave es w, la razón entre la presión de la energía
oscura y su densidad energética. A w < -1, el universo acabaría por ser
desgarrado. Primero, las galaxias se separarían entre sí, luego la gravedad
sería demasiado débil para mantener integrada cada galaxia. Los sistemas
planetarios perderían su cohesión gravitatoria. En los últimos minutos, se
desbaratarán estrellas y planetas, y los átomos serán destruidos.
Los autores de esta hipótesis calculan que el fin del tiempo
ocurriría aproximadamente 3,5×1010 años después del Big Bang, es decir, dentro
de 2,0×1010
Una modificación de esta teoría denominada Big Freeze,
aunque poco aceptada,[cita requerida] afirma que el universo continuaría su
expansión sin provocar un Big Rip.
 Añadiendo pérdidas de
energía, se consigue modelar una situación más próxima a la realidad. Así,
nótese que la oscilación descrita en el apartado anterior se prolongaría
indefinidamente en el tiempo (la sinusoide que describe la posición no converge
a cero en ningún momento). Una situación más verosímil se corresponde con la
presencia de una fuerza adicional que frena el movimiento. Esa fuerza puede ser
constante (pero siempre con signo tal que frene el movimiento). Es el caso de
rozamientos secos: la fuerza no depende ni de la velocidad ni de la posición.
Otra situación que se produce en la realidad es que la fuerza sea proporcional
a la velocidad elevada a una potencia, entera o no. Así sucede cuando la fuerza
que frena proviene de la viscosidad o de las pérdidas aerodinámicas. Se tratará
únicamente el caso más simple, es decir, cuando la fuerza sea proporcional a la
velocidad. En este caso la fuerza será:
Añadiendo pérdidas de
energía, se consigue modelar una situación más próxima a la realidad. Así,
nótese que la oscilación descrita en el apartado anterior se prolongaría
indefinidamente en el tiempo (la sinusoide que describe la posición no converge
a cero en ningún momento). Una situación más verosímil se corresponde con la
presencia de una fuerza adicional que frena el movimiento. Esa fuerza puede ser
constante (pero siempre con signo tal que frene el movimiento). Es el caso de
rozamientos secos: la fuerza no depende ni de la velocidad ni de la posición.
Otra situación que se produce en la realidad es que la fuerza sea proporcional
a la velocidad elevada a una potencia, entera o no. Así sucede cuando la fuerza
que frena proviene de la viscosidad o de las pérdidas aerodinámicas. Se tratará
únicamente el caso más simple, es decir, cuando la fuerza sea proporcional a la
velocidad. En este caso la fuerza será:




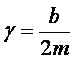






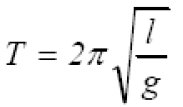










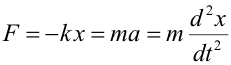










.jpg)









