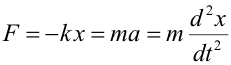Un movimiento armónico simple es el que describe una
partícula sometida a una fuerza restauradora proporcional a su desplazamiento.
Un movimiento armónico simple es el que describe una
partícula sometida a una fuerza restauradora proporcional a su desplazamiento.
F = - k x (Ley de Hooke)
Por ejemplo, el movimiento que describe una masa bajo la acción de la fuerza recuperadora del muelle o resorte:
La masa sujeta al muelle describe un movimiento oscilatorio.
Para calcular su aceleración utilizamos la Segunda Ley de Newton (F = ma):
Para calcular la posición o elongación (x) de la masa en función del tiempo (t) habría que resolver la ecuación diferencial anterior que relaciona la aceleración (a) con el desplazamiento (x).
Ecuaciones del movimiento armónico simple (utilizando la función COSENO):
La solución de la ecuación diferencial anterior es:
Definimos la frecuencia angular ω, cuyas unidades en el SI son rad/s, como:
La constante A que aparece en la expresión anterior se
denomina amplitud del movimiento, y es el máximo desplazamiento de la masa con
respecto a su posición de equilibrio x = 0. Sus unidades en el SI son los
metros (m).
El argumento del coseno (ωt+δ) es la fase y se mide en radianes, δ es la fase inicial, constante de fase o desfase y viene determinada por las condiciones iniciales del problema.
El tiempo que tarda la masa en efectuar una oscilación
completa se denomina periodo (T), y está relacionado con la frecuencia angular
mediante la expresión: ω = 2π/T
El número de oscilaciones que se realiza en un segundo se llama frecuencia (f) y se calcula como la inversa del periodo: f = 1/T Se mide en s-1 o Herzios (Hz)
El número de oscilaciones que se realiza en un segundo se llama frecuencia (f) y se calcula como la inversa del periodo: f = 1/T Se mide en s-1 o Herzios (Hz)
De la definición de frecuencia se obtiene que: ω = 2π f
La velocidad y la aceleración de una partícula que describe
un movimiento armónico simple se obtiene derivando la ecuación de la posición
en función del tiempo.
Ecuación de la posición en función del tiempo:
Ecuación de la velocidad en función del tiempo:
Ecuación de la aceleración en función del tiempo:
Velocidad (v) y aceleración (a) en función de la posición (x):
Posición, velocidad y aceleración de una partícula que
describe un movimiento armónico simple. δ es la constante de fase y viene determinada por las
condiciones iniciales del problema.
Sustituyendo x=0 obtenemos la velocidad máxima (vmáx = ωA) y la aceleración mínima (amín = 0)
Sustituyendo x=A obtenemos la velocidad mínima (vmín = 0) y la aceleración máxima (amáx = - ω2A)